LeetCode 90. 子集 II
作者:Choi Yang
更新于:3 个月前
字数统计:649 字
阅读时长:2 分钟
阅读量:
题目描述
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
javascript
输入: [1, 2, 2];
输出: [[2], [1], [1, 2, 2], [2, 2], [1, 2], []];输入: [1, 2, 2];
输出: [[2], [1], [1, 2, 2], [2, 2], [1, 2], []];来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/subsets-ii 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
本题还是挺有意思的,我们要求的是子集,但是子集要进行去重操作,采用的做法是先对原数组进行排序,那么排序后的数组重复的元素必定是相邻的,然后在遍历解空间树的时候,要做一个去重的操作,当遇到重复出现,也就是和前面相邻元素相同的时候,直接跳过该节点,不让它向下递归。具体示意图如下:
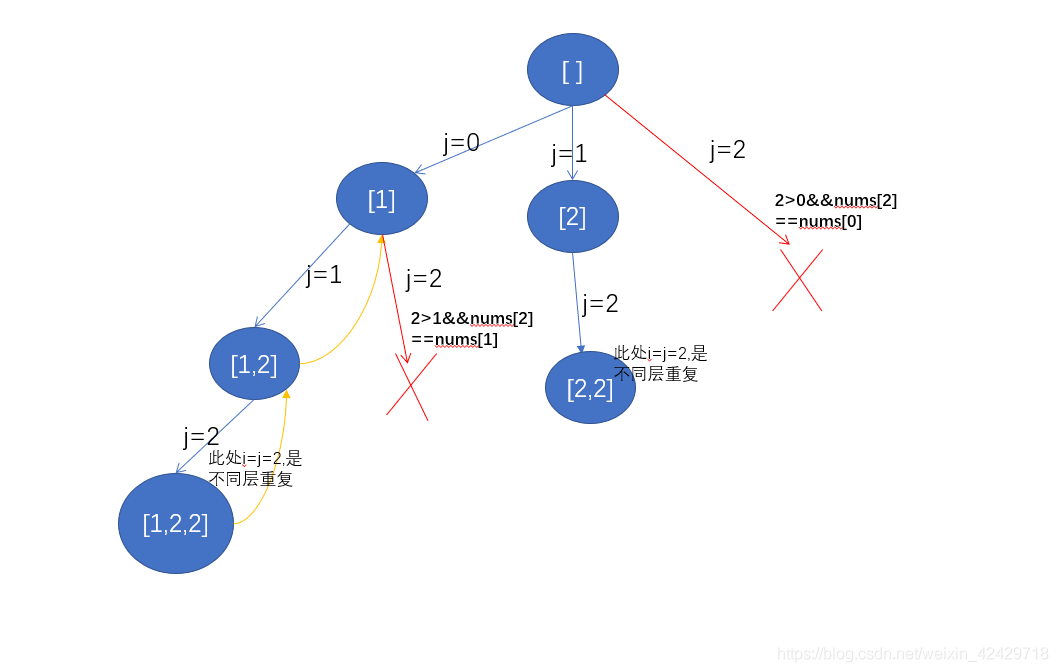
dfs的话,一条路会一直走下去,然后回溯回来,在走之前,start是当前层第一个元素,只有当前元素下标大于 start才会有重复元素,而对于不同层的重复元素,我们不应该切断,应该继续走,不然就不会有 [1,2,2]这样的子集出现了。
javascript
var subsetsWithDup = function (nums) {
let res = [];
nums.sort((a, b) => a - b);
let dfs = (t, start) => {
res.push(t);
for (let i = start; i < nums.length; i++) {
// 同层重复,跳过
if (i > start && nums[i - 1] == nums[i]) continue;
t.push(nums[i]);
dfs(t.slice(), i + 1);
t.pop();
}
};
dfs([], 0);
return res;
};var subsetsWithDup = function (nums) {
let res = [];
nums.sort((a, b) => a - b);
let dfs = (t, start) => {
res.push(t);
for (let i = start; i < nums.length; i++) {
// 同层重复,跳过
if (i > start && nums[i - 1] == nums[i]) continue;
t.push(nums[i]);
dfs(t.slice(), i + 1);
t.pop();
}
};
dfs([], 0);
return res;
};cpp
class Solution {
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
vector<vector<int>> res;
sort(nums.begin(), nums.end());
function<void(vector<int>, int)> dfs = <CustomLink title="&" href="vector<int> t, int start" /> {
res.push_back(t);
for (int i = start; i < nums.size(); i++) {
// 同层重复,跳过
if (i > start && nums[i - 1] == nums[i]) continue;
t.push_back(nums[i]);
dfs(t, i + 1);
t.pop_back();
}
};
dfs({}, 0);
return res;
}
};class Solution {
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
vector<vector<int>> res;
sort(nums.begin(), nums.end());
function<void(vector<int>, int)> dfs = <CustomLink title="&" href="vector<int> t, int start" /> {
res.push_back(t);
for (int i = start; i < nums.size(); i++) {
// 同层重复,跳过
if (i > start && nums[i - 1] == nums[i]) continue;
t.push_back(nums[i]);
dfs(t, i + 1);
t.pop_back();
}
};
dfs({}, 0);
return res;
}
};java
class Solution {
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
dfs(res, new ArrayList<>(), nums, 0);
return res;
}
private void dfs(List<List<Integer>> res, List<Integer> t, int[] nums, int start) {
res.add(new ArrayList<>(t));
for (int i = start; i < nums.length; i++) {
// 同层重复,跳过
if (i > start && nums[i - 1] == nums[i]) continue;
t.add(nums[i]);
dfs(res, t, nums, i + 1);
t.remove(t.size() - 1);
}
}
}class Solution {
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
dfs(res, new ArrayList<>(), nums, 0);
return res;
}
private void dfs(List<List<Integer>> res, List<Integer> t, int[] nums, int start) {
res.add(new ArrayList<>(t));
for (int i = start; i < nums.length; i++) {
// 同层重复,跳过
if (i > start && nums[i - 1] == nums[i]) continue;
t.add(nums[i]);
dfs(res, t, nums, i + 1);
t.remove(t.size() - 1);
}
}
}python
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
nums.sort()
def dfs(t, start):
res.append(t[:])
for i in range(start, len(nums)):
# 同层重复,跳过
if i > start and nums[i - 1] == nums[i]: continue
t.append(nums[i])
dfs(t, i + 1)
t.pop()
dfs([], 0)
return resclass Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
nums.sort()
def dfs(t, start):
res.append(t[:])
for i in range(start, len(nums)):
# 同层重复,跳过
if i > start and nums[i - 1] == nums[i]: continue
t.append(nums[i])
dfs(t, i + 1)
t.pop()
dfs([], 0)
return resjavascript
学如逆水行舟,不进则退学如逆水行舟,不进则退